Circle
A circle can be defined as a closed curved line on which every point is equally distant from a fixed point within it. Following is some of the terminology used in referring to a circle:
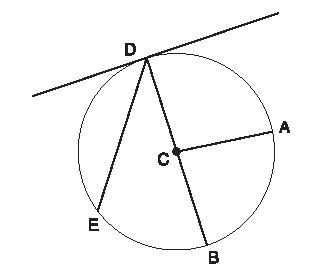
1. The fixed point is called the center of the circle (C in Figure 1).
2. A line segment joining the center to any point on the circle is the radius of the circle (CA in Figure 1).
3. A line segment passing through the center of the circle and joining any two points on the circle is the diameter of the circle (DB in Figure 1). The diameter of a circle is twice its radius.
4. The distance around the circle is called the circumference of the circle.
5. Any portion of the curved line that makes up the circle is an arc of the circle (for example, AB or DA in Figure 1).
6. A straight line inside the circle joining the two end points of an arc is a chord of the circle (DE in Figure 1).
Mathematical relationships
One of the interesting facts about circles is that the ratio between their circumference and their diameter is always the same, no matter what size the circle is. That ratio is given the name pi ( π ) and has the value of 3.141592+. Pi is an irrational number. That is, it cannot be expressed as the ratio of two whole numbers. The + added at the end of the value above means that the value of pi is indeterminate: you can continue to divide the circumference of any circle by its diameter forever and never get an answer without a remainder.
The area of any circle is equal to its radius squared multiplied by π , or: A = π r 2 . The circumference of a circle can be found by multiplying its diameter by π (C = π D) or twice its radius by π (C = 2πr).
Comment about this article, ask questions, or add new information about this topic: