Fractal

A fractal is a geometric figure with two special properties. First, it is irregular, fractured, fragmented, or loosely connected in appearance. Second, it is self-similar; that is, the figure looks much the same no matter how far away or how close up it is viewed.

The term fractal was invented by Polish French mathematician Benoit Mandelbrot (1924– ) in 1975. He took the word from the Latin word fractus, which means "broken."

The idea behind fractals is fairly simple and obvious when explained. But the mathematics used to develop those ideas is not so simple.

Natural fractals

Most objects in nature do not have simple geometric shapes. Clouds, trees, and mountains, for example, usually do not look like circles, triangles, or pyramids. Instead, they can best be described as fractals. Natural objects that can be described as fractals are called natural fractals.

One of the natural objects most often used to explain fractals is a coastline. A coastline has the three properties typical of any fractal figure. First, a coastline is irregular, consisting of bays, harbors, and peninsulas. By definition, any fractal must be irregular in shape.

Second, the irregularity is basically the same at all levels of magnification. Whether viewed from orbit high above Earth, from a helicopter, or from land, whether viewed with the naked eye, or a magnifying glass, every coastline is similar to itself. While the patterns are not precisely the same at each level of magnification, the essential features of a coastline are observed at each level. This property is the self-similar property that also is basic to all fractals.

Third, the length of a coastline depends on the magnification at which it is measured. Measuring the length of a coastline on a photograph taken from space will give only an estimate of its length. Many small bays and peninsulas will not appear, and the lengths of their perimeters will be excluded from the estimate. A better estimate can be obtained using a photograph taken from a helicopter. Some detail will still be missing, but many of the features missing in the space photo will be included. Thus, the estimate will be longer and closer to what might be termed the actual length of the coastline.

This estimate can be improved further by walking the coastline wearing a pedometer. Again, a longer measurement will result, perhaps more nearly equal to the actual length. But the result is still an estimate because many parts of a coastline are made up of rocks and pebbles that are smaller than the length of an average stride. Successively better estimates can be made by increasing the level of magnification, and each successive measurement will find the coastline longer. Eventually, the level of magnification must achieve atomic or even nuclear resolution to allow measurement of the irregularities in each grain of sand, each clump of dirt, and each tiny pebble, until the length appears to become infinite. This problematic result suggests the length of every coastline is the same.

The resolution of this problem requires that we rethink the way space is described. Standard one-dimensional space (such as a point), twodimensional space (such as a line), and three-dimensional space (such as a sphere) are not adequate for the analysis of fractals. Instead, nonintegral dimensions (1½; 2⅓; etc.) are needed.

Constructions

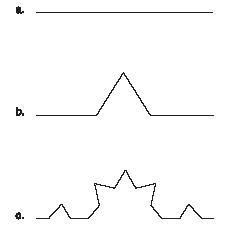
Fractals can often be drawn by rather simple rules, as shown in the accompanying illustration. This drawing shows how the pathway taken by a dust particle in air can be modeled by using fractals. We begin in Step A with a straight line. First, the center one-third of the line is removed and broken in half, as shown in Step B. Next, the center one-third of each of the three remaining line segments is removed and broken in half, as shown in Step C. This process is repeated over and over again until a fractal figure is formed that looks like the path followed by a dust particle in air.

Applications

The construction of a well-known fractal, the triadic Koch curve. A line segment (a) has its central one-third removed and replaced with a segment twice as long (b). In order to accomplish this, the replacement segment is "broken" in the middle. The resulting curve has four segments each one-third the length of the original line. Next, the center one-third of each of the four segments is replaced with a "broken" line twice as long as the segment that was removed (c). Now the curve has 16 segments, each one-ninth the length of the original line. Repeating this process indefinitely results in a Koch curve which is self-similar because any piece of it can be magnified by a factor of three and look the same as an unmagnified segment. (Reproduced by permission of

The Gale Group

.)

The similarity between fractals and natural objects has resulted in a number of important applications

for this field of mathematics. Fractals are used by geologists to model the meandering paths of rivers and the rock formations of mountains; by botanists to model the branching patterns of trees and shrubs; by astronomers to model the distribution of mass in the universe; by physiologists to model the human circulatory system; by physicists and engineers to model turbulence in fluids; and by economists to model the stock market and world economics.