Mass, Density, and Volume - Real-life applications

Atomic Mass Units
Chemists do not always deal in large units of mass, such as the mass of a human body—which, of course, is measured in kilograms. Instead, the chemist's work is often concerned with measurements of mass for the smallest types of matter: molecules, atoms, and other elementary particles. To measure these even in terms of grams (0.001 kg) is absurd: a single atom of carbon, for instance, has a mass of 1.99 · 10 −23 g. In other words, a gram is about 50,000,000,000,000,000,000,000 times larger than a carbon atom—hardly a usable comparison.
Instead, chemists use an atom mass unit (abbreviated amu), which is equal to 1.66 · 10 −24 g. Even so, is hard to imagine determining the mass of single atoms on a regular basis, so chemists make use of figures for the average atomic mass of a particular element. The average atomic mass of carbon, for instance, is 12.01 amu. As is the case with any average, this means that some atoms—different isotopes of carbon—may weigh more or less, but the figure of 12.01
- Hydrogen (H): 1.008 amu
- Helium (He): 4.003 amu
- Lithium (Li): 6.941 amu
- Nitrogen (N): 14.01 amu
- Oxygen (O): 16.00
- Aluminum (Al): 26.98
- Chlorine (Cl): 35.46 amu
- Gold (Au): 197.0 amu
- Hassium (Hs): [265 amu]
The figure for hassium, with an atomic number of 108, is given in brackets because this number is the mass for the longest-lived isotope. The average value of mass for the molecules in a given compound can also be rendered in terms of atomic mass units: water (H 2 O) molecules, for instance, have an average mass of 18.0153 amu. Molecules of magnesium oxide (MgO), which can be extracted from sea water and used in making ceramics, have an average mass much higher than for water: 40.304 amu.
These values are obtained simply by adding those of the atoms included in the molecule: since water has two hydrogen atoms and one oxygen, the average molecular mass is obtained by multiplying the average atomic mass of hydrogen by two, and adding it to the average atomic mass of oxygen. In the case of magnesium oxide, the oxygen is bonded to just one other atom—but magnesium, with an average atomic mass of 24.304, weighs much more than hydrogen.
Molar Mass
It is often important for a chemist to know exactly how many atoms are in a given sample, particularly in the case of a chemical reaction between two or more samples. Obviously, it is impossible to count atoms or other elementary particles, but there is a way to determine whether two items—regardless of the elements or compounds involved—have the same number of elementary particles. This method makes use of the figures for average atomic mass that have been established for each element.
If the average atomic mass of the substance is 5 amu, then there should be a very large number of atoms (if it is an element) or molecules (if it is a compound) of that substance having a total mass of 5 grams (g). Similarly, if the average atomic mass of the substance is 7.5 amu, then there should be a very large number of atoms or molecules of that substance having a total mass of 7.5 g. What is needed, clearly, is a very large number by which elementary particles must be multiplied in order to yield a mass whose value in grams is equal to the value, in amu, of its average atomic mass. This is known as Avogadro's number.
AVOGADRO'S NUMBER.
The first scientist to recognize a meaningful distinction between atoms and molecules was Italian physicist Amedeo Avogadro (1776-1856). Avogadro maintained that gases consisted of particles—which he called molecules—that in turn consisted of one or more smaller particles. He further reasoned that one liter of any gas must contain the same number of particles as a liter of another gas.
In order to discuss the behavior of molecules, it was necessary to set a large quantity as a basic unit, since molecules themselves are very small. This led to the establishment of what is known as Avogadro's number, equal to 6.022137 × 10 23 (more than 600 billion trillion.)
The magnitude of Avogadro's number is almost inconceivable. The same number of grains of sand would cover the entire surface of Earth at a depth of several feet. The same number of seconds, for instance, is about 800,000 times as long as the age of the universe (20 billion years). Avogadro's number—named after the man who introduced the concept of the molecule, but only calculated years after his death—serves a very useful purpose in computations involving molecules.
THE MOLE.
To compare two substances containing the same number of atoms or molecules, scientists use the mole, the SI fundamental unit for "amount of substance." A mole (abbreviated mol) is, generally speaking, Avogadro's number of atoms or molecules; however, in the more precise SI definition, a mole is equal to the number of carbon atoms in 12.01 g (0.03 lb) of carbon. Note that, as stated earlier, carbon has an average atomic mass of 12.01 amu. This is no coincidence, of course: multiplication of the average atomic mass by Avogadro's number yields a figure in grams equal to the value of the average atomic mass in amu.
The term "mole" can be used in the same way we use the word "dozen." Just as "a dozen" can refer to twelve cakes or twelve chickens, so "mole" always describes the same number of molecules. Just as one liter of water, or one liter of mercury, has a certain mass, a mole of any given substance has its own particular mass, expressed in grams. A mole of helium, for instance, has a mass of 4.003 g (0.01 lb), whereas a mole of iron is 55.85 g (0.12 lb) These figures represent the molar mass for each: that is, the mass of 1 mol of a given substance.
Once again, the value of molar mass in grams is the same as that of the average atomic mass in amu. Also, it should be clear that, given the fact that helium weighs much less than air—the reason why helium-filled balloons float—a quantity of helium with a mass of 4.003 g must be a great deal of helium. And indeed, as indicated earlier, the quantity of atoms or molecules in a mole is sufficiently great to make a sample that is large, but still usable for the purposes of study or comparison.
Measuring Volume
Mass, because of its fundamental nature, is sometimes hard to comprehend, and density requires an explanation in terms of mass and volume. Volume, on the other hand, appears to be quite straightforward—and it is, when one is describing a solid of regular shape. In other situations, however, volume measurement is more complicated.
As noted earlier, the volume of a cube can be obtained simply by multiplying length by width by height. There are other means for measuring the volume of other straight-sided objects, such as a pyramid. Still other formulae, which make use of the constant π (roughly equal to 3.14) are necessary for measuring the volume of a cylinder, a sphere, or a cone.
For an object that is irregular in shape, however, one may have to employ calculus—but the most basic method is simply to immerse the object in water. This procedure involves measuring the volume of the water before and after immersion, and calculating the difference. Of course, the object being measured cannot be water-soluble; if it is, its volume must be measured in a non-water-based liquid such as alcohol.
LIQUID AND GAS VOLUME.
Measuring liquid volumes is even easier than for solids, given the fact that liquids have no definite shape, and will simply take the shape of the container in which they are placed. Gases are similar to liquids in the sense that they expand to fit their container; however, measurement of gas volume is a more involved process than that used to measure either liquids or solids, because gases are highly responsive to changes in temperature and pressure.
If the temperature of water is raised from its freezing point to its boiling point—from 32°F (0°C) to 212°F (100°C)—its volume will increase by only 2%. If its pressure is doubled from 1 atm (defined as normal air pressure at sea level) to 2 atm, volume will decrease by only 0.01%. Yet if air were heated from 32° to 212°F, its volume would increase by 37%; if its pressure were doubled from 1 atm to 2, its volume would decrease by 50%.
Not only do gases respond dramatically to changes in temperature and pressure, but also, gas molecules tend to be non-attractive toward one another—that is, they tend not to stick together. Hence, the concept of "volume" in relation to a gas is essentially meaningless unless its temperature and pressure are known.
Comparing Densities
In the discussion of molar mass above, helium and iron were compared, and we saw that the mass of a mole of iron was about 14 times as great as that of a mole of helium. This may seem like a fairly small factor of difference between them: after all, helium floats on air, whereas iron (unless it is arranged in just the right way, for instance, in a tanker) sinks to the bottom of the ocean. But be careful: the comparison of molar mass is only an expression of the mass of a helium atom as compared to the mass of an iron atom. It makes no reference to density, which is the ratio of mass to volume.
Expressed in terms of the ratio of mass to volume, the difference between helium and iron becomes much more pronounced. Suppose, on the one hand, one had a gallon jug filled with iron. How many gallons of helium does it take to equal the mass of the iron? Fourteen? Try again: it takes more than 43,000 gallons of helium to equal the mass of the iron in one gallon jug! Clearly, what this shows is that the density of iron is much, much greater than that of helium.
This, of course, is hardly a surprising revelation; still, it is sometimes easy to get confused by comparisons of mass as opposed to comparisons of density. One might even get tricked by the old elementary-school brain-teaser that goes something like this: "Which is heavier, a ton of feathers or a ton of cannonballs?" Of course neither is heavier, but the trick element in the question relates to the fact that it takes a much greater volume of feathers (measured in cubic feet, for instance) than of cannonballs to equal a ton.
One of the interesting things about density, as distinguished from mass and volume, is that it has nothing to do with the amount of material. A kilogram of iron differs from 10 kg of iron both in mass and volume, but the density of both samples is the same. Indeed, as discussed below, the known densities of various materials make it possible to determine whether a sample of that material is genuine.
COMPARING DENSITIES.
As noted several times, the densities of numerous materials are known quantities, and can be easily compared. Some examples of density, all expressed in terms of grams per cubic centimeter, are listed below. These figures are measured at a temperature of 68°F (20°C), and for hydrogen and oxygen, the value was obtained at normal atmospheric pressure (1 atm):
Comparisons of Densities for Various Substances:
- Oxygen: 0.00133 g/cm 3
- Hydrogen: 0.000084 g/cm 3
- Ethyl alcohol: 0.79 g/cm 3
- Ice: 0.920 g/cm 3
- Water: 1.00 g/cm 3
- Concrete: 2.3 g/cm 3
- Iron: 7.87 g/cm 3
- Lead: 11.34 g/cm 3
- Gold: 19.32 g/cm 3
Specific Gravity
IS IT REALLY GOLD?
Note that pure water (as opposed to sea water, which is 3% more dense) has a density of 1.0 g per cubic centimeter. Water is thus a useful standard for measuring the specific gravity of other substances, or the ratio between the density of that substance and the density of water. Since the specific gravity of water is 1.00—also the density of water in g/cm 3 —the specific gravity of any substance (a number, rather than a number combined with a unit of measure) is the same as the value of its own density in g/cm 3 .
Comparison of densities make it possible to determine whether a piece of jewelry alleged to be solid gold is really genuine. To determine the answer, one must drop the sample in a beaker of water with graduated units of measure clearly marked. Suppose the item has a mass of 10 g. The density of gold is 19 g/cm 3 , and because density is equal to mass divided by volume, the volume of water displaced should be equal to the mass divided by the density. The latter figure is equal to 10 g divided by 19 g/cm 3 , or 0.53 ml. Suppose that instead, the item displaced 0.88 ml of water. Clearly it is not gold, but what is it?
Given the figures for mass and volume, its density is equal to 11.34 g/cm 3 —which happens to be the density of lead. If, on the other hand, the amount of water displaced were somewhere between the values for pure gold and pure lead, one could calculate what portion of the item was gold and which lead. It is possible, of course, that it could contain some other metal, but given the high specific gravity of lead, and the fact that its density is relatively close to that of gold, lead is a favorite gold substitute among jewelry counterfeiters.
SPECIFIC GRAVITY AND THE DENSITIES OF PLANETS.
Most rocks near the surface of Earth have a specific gravity somewhere between 2 and 3, while the specific gravity of the planet itself is about 5. How do scientists know that the density of Earth is around 5 g/cm 3 ? The computation is fairly simple, given the fact that the mass and volume of the planet are known. And given the fact that most of what lies close to Earth's surface—sea water, soil, rocks—has a specific gravity well below 5, it is clear that Earth's interior must contain high-density materials, such as nickel or iron. In the same way, calculations regarding the density of other objects in the Solar System provide a clue as to their interior composition.
This brings the discussion back around to a topic raised much earlier in this essay, when comparing the weight of a person on Earth versus that person's weight on the Moon. It so happens that the Moon is smaller than Earth, but that is not the reason it exerts less gravitational pull: as noted earlier, the gravitational force a planet, moon, or other body exerts is related to its mass, not its size.
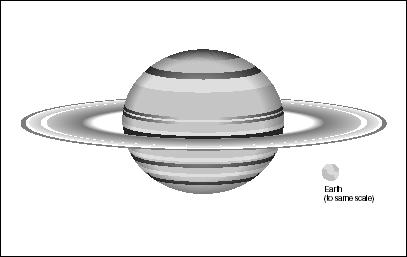
It so happens, too, that Jupiter is much larger than Earth, and that it exerts a gravitational pull much greater than that of Earth. This is because it has a mass many times as great as Earth's. But what about Saturn, the second-largest planet in the Solar System? In size it is only about 17% smaller than Jupiter, and both are much, much larger than Earth. Yet a person would weigh much less on Saturn than on Jupiter, because Saturn has a mass much smaller than Jupiter's. Given the close relation in size between the two planets, it is clear that Saturn has a much lower density than Jupiter, or in fact even Earth: the great ringed planet has a specific gravity of less than 1.
WHERE TO LEARN MORE
Chahrour, Janet. Flash! Bang! Pop! Fizz!: Exciting Science for Curious Minds. Illustrated by Ann Humphrey Williams. Hauppauge, NY: Barron's, 2000.
"Density and Specific Gravity" (Web site). <http://www.tpub.com/fluid/ch1e.htm> (March 27, 2001).
"Density, Volume, and Cola" (Web site). <http://student.biology.arizona.edu/sciconn/density/density_coke.html> (March 27, 2001).
Ebbing, Darrell D.; R. A. D. Wentworth; and James P. Birk. Introductory Chemistry. Boston: Houghton Mifflin, 1995.
"The Mass Volume Density Challenge" (Web site). <http://science-math-technology.com/mass_volume_density.html> (March 27, 2001).
"MegaConverter 2" (Web site). <http://www.megaconverter.com> (May 7, 2001).
"Metric Density and Specific Gravity" (Web site). <http://www.essex1.com/people/speer/density.html> (March 27, 2001).
Robson, Pam. Clocks, Scales and Measurements. New York: Gloucester Press, 1993.
"Volume, Mass, and Density" (Web site). <http://www.nyu.edu/pages/mathmol/modules/water/density_intro.html> (March 27, 2001).
Zumdahl, Steven S. Introductory Chemistry: A Foundation, 4th ed. Boston: Houghton Mifflin, 2000.
Comment about this article, ask questions, or add new information about this topic: