Frame of Reference - Real-life applications
Points and Graphs
There is no such thing as an absolute frame of reference—that is, a frame of reference that is fixed, and not dependent on anything else. If the entire universe consisted of just two points, it would be impossible (and indeed irrelevant) to say which was to the right of the other. There would be no right and left: in order to have such a distinction, it is necessary to have a third point from which to evaluate the other two points.
As long as there are just two points, there is only one dimension. The addition of a third point—as long as it does not lie along a straight line drawn through the first two points—creates two dimensions, length and width. From the frame of reference of any one point, then, it is possible to say which of the other two points is to the right.

Clearly, the judgment of right or left is relative, since it changes from point to point. A more absolute judgment (but still not a completely absolute one) would only be possible from the frame of reference of a fourth point. But to constitute a new dimension, that fourth point could not lie on the same plane as the other three points—more specifically, it should not be possible to create a single plane that encompasses all four points.
Assuming that condition is met, however, it then becomes easier to judge right and left. Yet right and left are never fully absolute, a fact easily illustrated by substituting people for points. One may look at two objects and judge which is to the right of the other, but if one stands on one's head, then of course right and left become reversed.
Of course, when someone is upside-down, the correct orientation of left and right is still fairly obvious. In certain situations observed by physicists and other scientists, however, orientation is not so simple. It then becomes necessary to assign values to various points, and for this, scientists use tools such as the Cartesian coordinate system.
COORDINATES AND AXES.
Though it is named after the French mathematician and philosopher René Descartes (1596-1650), who first described its principles, the Cartesian system owes at least as much to Pierre de Fermat (1601-1665). Fermat, a brilliant French amateur mathematician—amateur in the sense that he was not trained in mathematics, nor did he earn a living from that discipline—greatly developed the Cartesian system.
A coordinate is a number or set of numbers used to specify the location of a point on a line, on a surface such as a plane, or in space. In the Cartesian system, the x-axis is the horizontal line of reference, and the y-axis the vertical line of reference. Hence, the coordinate (0, 0) designates the point where the x-and y-axes meet. All numbers to the right of 0 on the x-axis, and above 0 on the y-axis, have a positive value, while those to the left of 0 on the x-axis, or below 0 on the y-axis have a negative value.
This version of the Cartesian system only accounts for two dimensions, however; therefore, a z-axis, which constitutes a line of reference for the third dimension, is necessary in three-dimensional graphs. The z-axis, too, meets the x-and y-axes at (0, 0), only now that point is designated as (0, 0, 0).
In the two-dimensional Cartesian system, the x-axis equates to "width" and the y-axis to "height." The introduction of a z-axis adds the dimension of "depth"—though in fact, length, width, and height are all relative to the observer's frame of reference. (Most representations of the three-axis system set the x-and y-axes along a horizontal plane, with the z-axis perpendicular to them.) Basic studies in physics, however, typically involve only the x-and y-axes, essential to plotting graphs, which, in turn, are integral to illustrating the behavior of physical processes.
THE TRIPLE POINT.
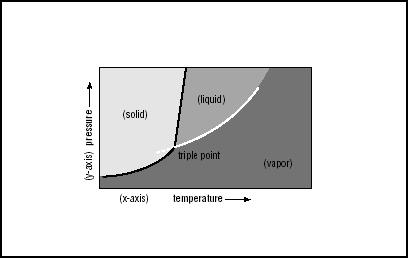
For instance, there is a phenomenon known as the "triple point," which is difficult to comprehend unless one sees it on a graph. For a chemical compound such as water or carbon dioxide, there is a point at which it is simultaneously a liquid, a solid, and a vapor. This, of course, seems to go against common sense, yet a graph makes it clear how this is possible.
Using the x-axis to measure temperature and the y-axis pressure, a number of surprises become apparent. For instance, most people associate water as a vapor (that is, steam) with very high temperatures. Yet water can also be a vapor—for example, the mist on a winter morning—at relatively low temperatures and pressures, as the graph shows.
The graph also shows that the higher the temperature of water vapor, the higher the pressure will be. This is represented by a line that curves upward to the right. Note that it is not a straight line along a 45° angle: up to about 68°F (20°C), temperature increases at a somewhat greater rate than pressure does, but as temperature gets higher, pressure increases dramatically.
As everyone knows, at relatively low temperatures water is a solid—ice. Pressure, however, is relatively high: thus on a graph, the values of temperatures and pressure for ice lie above the vaporization curve, but do not extend to the right of 32°F (0°C) along the x-axis. To the right of 32°F, but above the vaporization curve, are the coordinates representing the temperature and pressure for water in its liquid state.
Water has a number of unusual properties, one of which is its response to high pressures and low temperatures. If enough pressure is applied, it is possible to melt ice—thus transforming it from a solid to a liquid—at temperatures below the normal freezing point of 32°F. Thus, the line that divides solid on the left from liquid on the right is not exactly parallel to the y-axis: it slopes gradually toward the y-axis, meaning that at ultra-high pressures, water remains liquid even though it is well below the freezing point.
Nonetheless, the line between solid and liquid has to intersect the vaporization curve somewhere, and it does—at a coordinate slightly above freezing, but well below normal atmospheric pressure. This is the triple point, and though "common sense" might dictate that a thing cannot possibly be solid, liquid, and vapor all at once, a graph illustrating the triple point makes it clear how this can happen.
Numbers
In the above discussion—and indeed throughout this book—the existence of the decimal, or base-10,
Each numeration system has its own frame of reference, which is typically related to aspects of the human body. Thus throughout the course of history, some societies have developed a base-2 system based on the two hands or arms of a person. Others have used the fingers on one hand (base-5) as their reference point, or all the fingers and toes (base-20). The system in use throughout most of the world today takes as its frame of reference the ten fingers used for basic counting.
COEFFICIENTS.
Numbers, of course, provide a means of assigning relative values to a variety of physical characteristics: length, mass, force, density, volume, electrical charge, and so on. In an expression such as "10 meters," the numeral 10 is a coefficient, a number that serves as a measure for some characteristic or property. A coefficient may also be a factor against which other values are multiplied to provide a desired result.
For instance, the figure 3.141592, better known as pi (π), is a well-known coefficient used in formulae for measuring the circumference or area of a circle. Important examples of coefficients in physics include those for static and sliding friction for any two given materials. A coefficient is simply a number—not a value, as would be the case if the coefficient were a measure of something.
Standards of Measurement
Numbers and coefficients provide a convenient lead-in to the subject of measurement, a practical example of frame of reference in all sciences—and indeed, in daily life. Measurement always requires a standard of comparison: something that is fixed, against which the value of other things can be compared. A standard may be arbitrary in its origins, but once it becomes fixed, it provides a frame of reference.
Lines of longitude, for instance, are measured against an arbitrary standard: the "Prime Meridian" running through Greenwich, England. An imaginary line drawn through that spot marks the line of reference for all longitudinal measures on Earth, with a value of 0°. There is nothing special about Greenwich in any profound scientific sense; rather, its place of importance reflects that of England itself, which ruled the seas and indeed much of the world at the time the Prime Meridian was established.
The Equator, on the other hand, has a firm scientific basis as the standard against which all lines of latitude are measured. Yet today, the coordinates of a spot on Earth's surface are given in relation to both the Equator and the Prime Meridian.
CALIBRATION.
Calibration is the process of checking and correcting the performance of a measuring instrument or device against the accepted standard. America's preeminent standard for the exact time of day, for instance, is the United States Naval Observatory in Washington, D.C. Thanks to the Internet, people all over the country can easily check the exact time, and correct their clocks accordingly.
There are independent scientific laboratories responsible for the calibration of certain instruments ranging from clocks to torque wrenches, and from thermometers to laser beam power analyzers. In the United States, instruments or devices with high-precision applications—that is, those used in scientific studies, or by high-tech industries—are calibrated according to standards established by the National Institute of Standards and Technology (NIST).
THE VALUE OF STANDARDIZATION TO A SOCIETY.
Standardization of weights and measures has always been an important function of government. When Ch'in Shih-huang-ti (259-210 B.C. ) united China for the first time, becoming its first emperor, he set about standardizing units of measure as a means of providing greater unity to the country—thus making it easier to rule.
More than 2,000 years later, another empire—Russia—was negatively affected by its failure to adjust to the standards of technologically advanced nations. The time was the early twentieth century, when Western Europe was moving forward at a rapid pace of industrialization. Russia, by contrast, lagged behind—in part because its failure to adopt Western standards put it at a disadvantage.
Train travel between the West and Russia was highly problematic, because the width of railroad tracks in Russia was different than in Western Europe. Thus, adjustments had to be performed on trains making a border crossing, and this created difficulties for passenger travel. More importantly, it increased the cost of transporting freight from East to West.
Russia also used the old Julian calendar, as opposed to the Gregorian calendar adopted throughout much of Western Europe after 1582. Thus October 25, 1917, in the Julian calendar of old Russia translated to November 7, 1917 in the Gregorian calendar used in the West. That date was not chosen arbitrarily: it was then that Communists, led by V. I. Lenin, seized power in the weakened former Russian Empire.
METHODS OF DETERMINING STANDARDS.
It is easy to understand, then, why governments want to standardize weights and measures—as the U.S. Congress did in 1901, when it established the Bureau of Standards (now NIST) as a nonregulatory agency within the Commerce Department. Today, NIST maintains a wide variety of standard definitions regarding mass, length, temperature, and so forth, against which other devices can be calibrated.
Note that NIST keeps on hand definitions rather than, say, a meter stick or other physical model. When the French government established the metric system in 1799, it calibrated the value of a kilogram according to what is now known as the International Prototype Kilogram, a platinum-iridium cylinder housed near Sévres in France. In the years since then, the trend has moved away from such physical expressions of standards, and toward standards based on a constant figure. Hence, the meter is defined as the distance light travels in a vacuum (an area of space devoid of air or other matter) during the interval of 1/299,792,458 of a second.
METRIC VS. BRITISH.
Scientists almost always use the metric system, not because it is necessarily any less arbitrary than the British or English system (pounds, feet, and so on), but because it is easier to use. So universal is the metric system within the scientific community that it is typically referred to simply as SI, an abbreviation of the French Système International d'Unités —that is, "International System of Units."
The British system lacks any clear frame of reference for organizing units: there are 12 inches in a foot, but 3 feet in a yard, and 1,760 yards in a mile. Water freezes at 32°F instead of 0°, as it does in the Celsius scale associated with the metric system. In contrast to the English system, the metric system is neatly arranged according to the base-10 numerical framework: 10 millimeters to a centimeter, 100 centimeters to a meter, 1,000 meters to kilometer, and so on.
The difference between the pound and the kilogram aptly illustrates the reason scientists in general, and physicists in particular, prefer the metric system. A pound is a unit of weight, meaning that its value is entirely relative to the gravitational pull of the planet on which it is measured. A kilogram, on the other hand, is a unit of mass, and does not change throughout the universe. Though the basis for a kilogram may not ultimately be any more fundamental than that for a pound, it measures a quality that—unlike weight—does not vary according to frame of reference.
Frame of Reference in Classical Physics and Astronomy
Mass is a measure of inertia, the tendency of a body to maintain constant velocity. If an object is at rest, it tends to remain at rest, or if in motion, it tends to remain in motion unless acted upon by some outside force. This, as identified by the first law of motion, is inertia—and the greater the inertia, the greater the mass.
Physicists sometimes speak of an "inertial frame of reference," or one that has a constant velocity—that is, an unchanging speed and direction. Imagine if one were on a moving bus at constant velocity, regularly tossing a ball in the air and catching it. It would be no more difficult to catch the ball than if the bus were standing still, and indeed, there would be no way of determining, simply from the motion of the ball itself, that the bus was moving.
But what if the inertial frame of reference suddenly became a non-inertial frame of reference—in other words, what if the bus slammed on its brakes, thus changing its velocity? While the bus was moving forward, the ball was moving along with it, and hence, there was no relative motion between them. By stopping, the bus responded to an "outside" force—that is, its brakes. The ball, on the other hand, experienced that force indirectly. Hence, it would continue to move forward as before, in accordance with its own inertia—only now it would be in motion relative to the bus.
ASTRONOMY AND RELATIVE MOTION.
The idea of relative motion plays a powerful role in astronomy. At every moment, Earth is turning on its axis at about 1,000 MPH (1,600 km/h) and hurtling along its orbital path around the Sun at the rate of 67,000 MPH (107,826 km/h.) The fastest any human being—that is, the astronauts taking part in the Apollo missions during the late 1960s—has traveled is about 30% of Earth's speed around the Sun.
Yet no one senses the speed of Earth's movement in the way that one senses the movement of a car—or indeed the way the astronauts perceived their speed, which was relative to the Moon and Earth. Of course, everyone experiences the results of Earth's movement—the change from night to day, the precession of the seasons—but no one experiences it directly. It is simply impossible, from the human frame of reference, to feel the movement of a body as large as Earth—not to mention larger progressions on the part of the Solar System and the universe.
FROM ASTRONOMY TO PHYSICS.
The human body is in an inertial frame of reference with regard to Earth, and hence experiences no relative motion when Earth rotates or moves through space. In the same way, if one were traveling in a train alongside another train at constant velocity, it would be impossible to perceive that either train was actually moving—unless one referred to some fixed point, such as the trees or mountains in the background. Likewise, if two trains were sitting side by side, and one of them started to move, the relative motion might cause a person in the stationary train to believe that his or her train was the one moving.
For any measurement of velocity, and hence, of acceleration (a change in velocity), it is essential to establish a frame of reference. Velocity and acceleration, as well as inertia and mass, figured heavily in the work of Galileo Galilei (1564-1642) and Sir Isaac Newton (1642-1727), both of whom may be regarded as "founding fathers" of modern physics. Before Galileo, however, had come Nicholas Copernicus (1473-1543), the first modern astronomer to show that the Sun, and not Earth, is at the center of "the universe"—by which people of that time meant the Solar System.
In effect, Copernicus was saying that the frame of reference used by astronomers for millennia was incorrect: as long as they believed Earth to be the center, their calculations were bound to be wrong. Galileo and later Newton, through their studies in gravitation, were able to prove Copernicus's claim in terms of physics.
At the same time, without the understanding of a heliocentric (Sun-centered) universe that he inherited from Copernicus, it is doubtful that Newton could have developed his universal law of gravitation. If he had used Earth as the center-point for his calculations, the results would have been highly erratic, and no universal law would have emerged.
Relativity
For centuries, the model of the universe developed by Newton stood unchallenged, and even today it identifies the basic forces at work when speeds are well below that of the speed of light. However, with regard to the behavior of light itself—which travels at 186,000 mi (299,339 km) a second—Albert Einstein (1879-1955) began to observe phenomena that did not fit with Newtonian mechanics. The result of his studies was the Special Theory of Relativity, published in 1905, and the General Theory of Relativity, published a decade later. Together these altered humanity's view of the universe, and ultimately, of reality itself.
Einstein himself once offered this charming explanation of his epochal theory: "Put your hand on a hot stove for a minute, and it seems like an hour. Sit with a pretty girl for an hour, and it seems like a minute. That's relativity." Of course, relativity is not quite as simple as that—though the mathematics involved is no more challenging than that of a high-school algebra class. The difficulty lies in comprehending how things that seem impossible in the Newtonian universe become realities near the speed of light.
PLAYING TRICKS WITH TIME.
An exhaustive explanation of relativity is far beyond the scope of the present discussion. What is important is the central precept: that no measurement of space or time is absolute, but depends on the relative motion of the observer (that is, the subject) and the observed (the object). Einstein further established that the movement of time itself is relative rather than absolute, a fact that would become apparent at speeds close to that of light. (His theory also showed that it is impossible to surpass that speed.)
Imagine traveling on a spaceship at nearly the speed of light while a friend remains stationary on Earth. Both on the spaceship and at the friend's house on Earth, there is a TV camera trained on a clock, and a signal relays the image from space to a TV monitor on Earth, and vice versa. What the TV monitor reveals is surprising: from your frame of reference on the spaceship, it seems that time is moving more slowly for your friend on Earth than for you. Your friend thinks exactly the same thing—only, from the friend's perspective, time on the spaceship is moving more slowly than time on Earth. How can this happen?
Again, a full explanation—requiring reference to formulae regarding time dilation, and so on—would be a rather involved undertaking. The short answer, however, is that which was stated above: no measurement of space or time is absolute, but each depends on the relative motion of the observer and the observed. Put another way, there is no such thing as absolute motion, either in the three dimensions of space, or in the fourth dimension identified by Einstein, time. All motion is relative to a frame of reference.
RELATIVITY AND ITS IMPLICATIONS.
The ideas involved in relativity have been verified numerous times, and indeed the only reason why they seem so utterly foreign to most people is that humans are accustomed to living within the Newtonian framework. Einstein simply showed that there is no universal frame of reference, and like a true scientist, he drew his conclusions entirely from what the data suggested. He did not form an opinion, and only then seek the evidence to confirm it, nor did he seek to extend the laws of relativity into any realm beyond that which they described.
Yet British historian Paul Johnson, in his unorthodox history of the twentieth century, Modern Times (1983; revised 1992), maintained that a world disillusioned by World War I saw a moral dimension to relativity. Describing a set of tests regarding the behavior of the Sun's rays around the planet Mercury during an eclipse, the book begins with the sentence: "The modern world began on 29 May 1919, when photographs of a solar eclipse, taken on the Island of Principe off West Africa and at Sobral in Brazil, confirmed the truth of a new theory of the universe."
As Johnson went on to note,"…for most people, to whom Newtonian physics… were perfectly comprehensible, relativity never became more than a vague source of unease. It was grasped that absolute time and absolute length had been dethroned…. All at once, nothing seemed certain in the spheres…. At the beginning of the 1920s the belief began to circulate, for the first time at a popular level, that there were no longer any absolutes: of time and space, of good and evil, of knowledge, above all of value. Mistakenly but perhaps inevitably, relativity became confused with relativism."
Certainly many people agree that the twentieth century—an age that saw unprecedented mass murder under the dictatorships of Adolf Hitler and Josef Stalin, among others—was characterized by moral relativism, or the belief that there is no right or wrong. And just as Newton's discoveries helped usher in the Age of Reason, when thinkers believed it was possible to solve any problem through intellectual effort, it is quite plausible that Einstein's theory may have had this negative moral effect.
If so, this was certainly not Einstein's intention. Aside from the fact that, as stated, he did not set out to describe anything other than the physical behavior of objects, he continued to believe that there was no conflict between his ideas and a belief in an ordered universe: "Relativity," he once said, "teaches us the connection between the different descriptions of one and the same reality."
WHERE TO LEARN MORE
Beiser, Arthur. Physics, 5th ed. Reading, MA: Addison-Wesley, 1991.
Fleisher, Paul. Relativity and Quantum Mechanics: Principles of Modern Physics. Minneapolis, MN: Lerner Publications, 2002.
"Frame of Reference" (Web site). <http://www.physics.reading.ac.uk/units/flap/glossary/ff/frameref.html> (March 21, 2001).
"Inertial Frame of Reference" (Web site). <http://id.mind.net/~zona/mstm/physics/mechanics/framesOfReference/inertialFrame.html> (March 21, 2001).
Johnson, Paul. Modern Times: The World from the Twenties to the Nineties. Revised edition. New York: HarperPerennial, 1992.
King, Andrew. Plotting Points and Position. Illustrated by Tony Kenyon. Brookfield, CT: Copper Beech Books, 1998.
Parker, Steve. Albert Einstein and Relativity. New York: Chelsea House, 1995.
Robson, Pam. Clocks, Scales, and Measurements. New York: Gloucester Press, 1993.
Rutherford, F. James; Gerald Holton; and Fletcher G. Watson. Project Physics. New York: Holt, Rinehart, and Winston, 1981.
Swisher, Clarice. Relativity: Opposing Viewpoints. San Diego, CA: Greenhaven Press, 1990.
Comment about this article, ask questions, or add new information about this topic: