Gravity and Gravitation - How it works

Aristotle's Model

Greek philosophers of the period from the sixth to the fourth century B.C. grappled with a variety of questions concerning the fundamental nature of physical reality, and the forces that bind that reality into a whole. Among the most advanced thinkers of that period was Democritus (c. 460-370 B.C. ), who put forth a hypothesis many thousands of years ahead of its time: that all of matter interacts at the atomic level.

Aristotle (384-322 B.C. ), however, rejected the explanation offered by Democritus, an unfortunate circumstance given the fact that the great philosopher exerted an incalculable influence on the development of scientific thought. Aristotle's contributions to the advancement of the sciences were many and varied, yet his influence in physics was at least as harmful as it was beneficial. Furthermore, the fact that intellectual progress began slowing after several fruitful centuries of development in Greece only compounded the error. By the time civilization had reached the Middle Ages (c. 500 A.D. ) the Aristotelian model of physical reality had been firmly established, and an entire millennium passed before it was successfully challenged.

Wrong though it was in virtually all particulars, the Aristotelian system offered a comforting symmetry amid the troubled centuries of the early medieval period. It must have been reassuring indeed to believe that the physical universe was as simple as the world of human affairs was complex. According to this neat model, all materials on Earth consisted of four elements: earth, water, air, and fire.

Each element had its natural place. Hence, earth was always the lowest, and in some places, earth was covered by water. Water must then be higher, but clearly air was higher still, since it covered earth and water. Highest of all was fire, whose natural place was in the skies above the air. Reflecting these concentric circles were the orbits of the Sun, the Moon, and the five known planets. Their orbital paths, in the Aristotelian model of the universe—a model developed to a great degree by the astronomer Ptolemy (c. 100-170)—were actually spheres that revolved around Earth with clockwork precision.

On Earth, according to the Aristotelian model, objects tended to fall toward the ground in accordance with the admixtures of differing

elements they contained. A rock, for instance, was mostly earth, and hence it sought its own level, the lowest of all four elements. For the same reason, a burning fire rose, seeking the heights that were fire's natural domain. It followed from this that an object falls faster or slower, depending on the relative mixtures of elements in it: or, to use more modern terms, the heavier the object, the faster it falls.

Galileo Takes Up the Copernican Challenge

Over the centuries, a small but significant body of scientists and philosophers—each working independent from the other but building on the ideas of his predecessors—slowly began chipping away at the Aristotelian framework. The pivotal challenge came in the early part of the century, and the thinker who put it forward was not a physicist but an astronomer: Nicolaus Copernicus (1473-1543.)

Based on his study of the planets, Copernicus offered an entirely new model of the universe, one that placed the Sun and not Earth at its center. He was not the first to offer such an idea: half a century after Aristotle's death, Aristarchus (fl. 270 B.C. ) had a similar idea, but Ptolemy rejected his heliocentric (Sun-centered) model in favor of the geocentric or Earth-centered one. In subsequent centuries, no less a political authority than the Catholic Church gave its approval to the Ptolemaic system. This system seemed to fit well with a literal interpretation of biblical passages concerning God's relationship with man, and man's relationship to the cosmos; hence, the heliocentric model of Copernicus constituted an offense to morality.

For this reason, Copernicus was hesitant to defend his ideas publicly, yet these concepts found their way into the consciousness of European thinkers, causing a paradigm shift so fundamental that it has been dubbed "the Copernican Revolution." Still, Copernicus offered no explanation as to why the planets behaved as they did: hence, the true leader of the Copernican Revolution was not Copernicus himself but Galileo Galilei (1564-1642.)

Initially, Galileo set out to study and defend the ideas of Copernicus through astronomy, but soon the Church forced him to recant. It is said that after issuing a statement in which he refuted the proposition that Earth moves—a direct attack on the static harmony of the Aristotelian/Ptolemaic model—he protested in private:" E pur si muove!" (But it does move!) Placed under house arrest by authorities from Rome, he turned his attention to an effort that, ironically, struck the fatal blow against the old model of the cosmos: a proof of the Copernican system according to the laws of physics.

GRAVITATIONAL ACCELERATION.

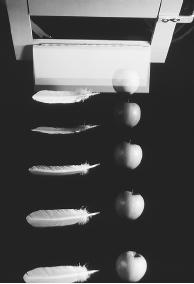
In the process of defending Copernicus, Galileo actually inaugurated the modern history of physics as a science (as opposed to what it had been during the Middle Ages: a nest of suppositions masquerading as knowledge). Specifically, Galileo set out to test the hypothesis that objects fall as they do, not because of their weight, but as a consequence of gravitational force. If this were so, the acceleration of falling bodies would have to be the same, regardless of weight. Of course, it was clear that a stone fell faster than a feather, but Galileo reasoned that this was a result of factors other than weight, and later investigations confirmed that air resistance and friction, not weight, are responsible for this difference.

On the other hand, if one drops two objects that have similar air resistance but differing weight—say, a large stone and a smaller one—they fall at almost exactly the same rate. To test this directly, however, would have been difficult for Galileo: stones fall so fast that, even if dropped from a great height, they would hit the ground too soon for their rate of fall to be tested with the instruments then available.

Instead, Galileo used the motion of a pendulum, and the behavior of objects rolling or sliding down inclined planes, as his models. On the basis of his observations, he concluded that all bodies are subject to a uniform rate of gravitational acceleration, later calibrated at 32 ft (9.8 m) per second. What this means is that for every 32 ft an object falls, it is accelerating at a rate of 32 ft per second as well; hence, after 2 seconds, it falls at the rate of 64 ft (19.6 m) per second; after 3 seconds, at 96 ft (29.4 m) per second, and so on.

Newton Discovers the Principle of Gravity

Building on the work of his distinguished fore-bear, Sir Isaac Newton (1642-1727)—who, incidentally, was born the same year Galileo died—developed a paradigm for gravitation that, even today, explains the behavior of objects in virtually all situations throughout the universe. Indeed, the Newtonian model reigned until the early

twentieth century, when Albert Einstein (1879-1955) challenged it on certain specifics.

Even so, Einstein's relativity did not disprove the Newtonian system as Copernicus and Galileo disproved Aristotle's and Ptolemy's theories; rather, it showed the limitations of Newtonian mechanics for describing the behavior of certain objects and phenomena. However, in the ordinary world of day-to-day experience—the world in which stones drop and heavy objects are hard to lift—the Newtonian system still offers the key to how and why things work as they do. This is particularly the case with regard to gravity and gravitation.

Like Galileo, Newton began in part with the aim of testing hypotheses put forth by an astronomer—in this case Johannes Kepler (1571-1630). In the early years of the seventeenth century, Kepler published his three laws of planetary motion, which together identified the elliptical (oval-shaped) path of the planets around the Sun. Kepler had discovered a mathematical relationship that connected the distances of the planets from the Sun to the period of their revolution around it. Like Galileo with Copernicus, Newton sought to generalize these principles to explain, not only how the planets moved, but also why they did.

Almost everyone has heard the story of Newton and the apple—specifically, that while he was sitting under an apple tree, a falling apple struck him on the head, spurring in him a great intuitive leap that led him to form his theory of gravitation. One contemporary biographer, William Stukely, wrote that he and Newton were sitting in a garden under some apple trees when Newton told him that "…he was just in the same situation, as when formerly, the notion of gravitation came into his mind. It was occasion'd by the fall of an apple, as he sat in a contemplative mood. Why should that apple always descend perpendicularly to the ground, he thought to himself. Why should it not go sideways or upwards, but constantly to the earth's centre?"

The tale of Newton and the apple has become a celebrated myth, rather like that of George Washington and the cherry tree. It is an embellishment of actual events: Newton never said that an apple hit him on the head, just that he was thinking about the way that apples fell. Yet the story has become symbolic of the creative intellectual process that occurs when a thinker makes a vast intuitive leap in a matter of moments. Of course, Newton had spent many years contemplating these ideas, and their development required great effort. What is important is that he brought together the best work of his predecessors, yet transcended all that had gone before—and in the process, forged a model that explained a great deal about how the universe functions.

The result was his Philosophiae Naturalis Principia Mathematica, or "Mathematical Principles of Natural Philosophy." Published in 1687, the book—usually referred to simply as the Principia —was one of the most influential works ever written. In it, Newton presented his three laws of motion, as well as his law of universal gravitation.

The latter stated that every object in the universe attracts every other one with a force proportional to the masses of each, and inversely proportional to the square of the distance between them. This statement requires some clarification with regard to its particulars, after which it will be reintroduced as a mathematical formula.

MASS AND FORCE.

The three laws of motion are a subject unto themselves, covered elsewhere in this volume. However, in order to understand gravitation, it is necessary to understand at least a few rudimentary concepts relating to them. The first law identifies inertia as the tendency of an object in motion to remain in motion, and of an object at rest to remain at rest. Inertia is measured by mass, which—as the second law states—is a component of force.

Specifically, the second law of motion states that force is equal to mass multiplied by acceleration. This means that there is an inverse relationship between mass and acceleration: if force remains constant and one of these factors increases, the other must decrease—a situation that will be discussed in some depth below.

Also, as a result of Newton's second law, it is possible to define weight scientifically. People typically assume that mass and weight are the same, and indeed they are on Earth—or at least, they are close enough to be treated as comparable factors. Thus, tables of weights and measures show that a kilogram, the metric unit of mass, is equal to 2.2 pounds, the latter being the principal unit of weight in the British system.

In fact, this is—if not a case of comparing to apples to oranges—certainly an instance of comparing apples to apple pies. In this instance, the kilogram is the "apple" (a fitting Newtonian metaphor!) and the pound the "apple pie." Just as an apple pie contains apples, but other things as well, the pound as a unit of force contains an additional factor, acceleration, not included in the kilo.

BRITISH VS. SI UNITS.

Physicists universally prefer the metric system, which is known in the scientific community as SI (an abbreviation of the French Système International d'Unités —that is, "International System of Units"). Not only is SI much more convenient to use, due to the fact that it is based on units of 10; but in discussing gravitation, the unequal relationship between kilograms and pounds makes conversion to British units a tedious and ultimately useless task.

Though Americans prefer the British system to SI, and are much more familiar with pounds than with kilos, the British unit of mass—called the slug—is hardly a household word. By contrast, scientists make regular use of the SI unit of force—named, appropriately enough, the newton. In the metric system, a newton (N) is the amount of force required to accelerate 1 kilogram of mass by 1 meter per second squared (m/s ² ) Due to the simplicity of using SI over the British system, certain aspects of the discussion below will be presented purely in terms of SI. Where appropriate, however, conversion to British units will be offered.

CALCULATING GRAVITATIONAL FORCE.

The law of universal gravitation can be stated as a formula for calculating the gravitational attraction between two objects of a certain mass, m ₁ AND M ₂ : F _grav = G · ( m ₁ M ₂ )/R ² . F _grav is gravitational force, and r ² the square of the distance between m ₁ and m ₂ .

As for G, in Newton's time the value of this number was unknown. Newton was aware simply that it represented a very small quantity: without it, ( m ₁ m ₂ )/ r ² could be quite sizeable for objects of relatively great mass separated by a relatively small distance. When multiplied by this very small number, however, the gravitational attraction would be revealed to be very small as well. Only in 1798, more than a century after Newton's writing, did English physicist Henry Cavendish (1731-1810) calculate the value of G.

As to how Cavendish derived the figure, that is an exceedingly complex subject far beyond the scope of the present discussion. Even to identify G as a number is a challenging task. First of all, it is a unit of force multiplied by squared area, then divided by squared mass: in other words, it is expressed in terms of (N · m ² )/kg ² , where N stands for newtons, m for meters, and kg for kilograms. Nor is the coefficient, or numerical value, of G a whole number such as 1. A figure as large as 1, in fact, is astronomically huge compared to G, whose coefficient is 6.67 · 10 ⁻¹¹ —in other words, 0.0000000000667.