Complex numbers

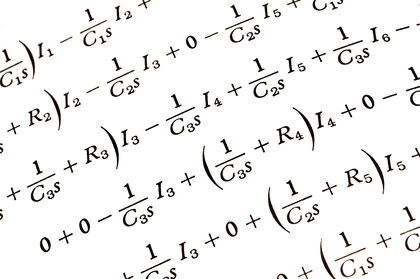
Complex numbers are numbers that consist of two parts, one real and one imaginary. An imaginary number is the square root of a real number, such as √−4;. The expression √−4 is said to be imaginary because no real number can satisfy the condition stated. That is, there is no number that can be squared to give the value −4, which is what √−4 means. The imaginary number √−1 has a special designation in mathematics. It is represented by the letter i.

Complex numbers can be represented as a binomial (a mathematical expression consisting of one term added to or subtracted from another) of the form a + bi. In this binomial, a and b represent real numbers and i = √−1. Some examples of complex numbers are 3 − i, ½ + 7i, and −6 − 2i.

The two parts of a complex number cannot be combined. Even though the parts are joined by a plus sign, the addition cannot be performed. The expression must be left as an indicated sum.

History

One of the first mathematicians to realize the need for complex numbers was Italian mathematician Girolamo Cardano (1501–1576). Around 1545, Cardano recognized that his method of solving cubic equations often led to solutions containing the square root of negative numbers. Imaginary numbers did not fully become a part of mathematics, however, until they were studied at length by French-English mathematician Abraham De Moivre (1667–1754), a Swiss family of mathematicians named the Bernoullis, Swiss mathematician Leonhard Euler (1707–1783), and others in the eighteenth century.

Arithmetic

In many ways, operations with complex numbers follow the same rules as those for real numbers. Two exceptions to those rules arise because of the nature of complex numbers. First, what appears to be an addition operation, a + bi, must be left uncombined. Second, the general expression

for any imaginary number, such as i ² = −1, violates the rule that the product of two numbers of a like sign is positive.

The general rules for working with complex numbers are as follows:

1. Equality: To be equal, two complex numbers must have equal real parts and equal imaginary parts. That is, assume that we know that the expressions (a + bi) and (c + di) are equal. That condition can be true if and only if a = c and b = d.

2. Addition: To add two complex numbers, the real parts and the imaginary parts are added separately. The following examples illustrate this rule:

(a + bi) + (c + di) = (a + c) + (b + d)i

(3 + 5i) + (8 − 7i) = 11 − 2i

3. Subtraction: To subtract a complex number, subtract the real part from the real part and the imaginary part from the imaginary part. For example:

(a + bi) − (c + di) = (a − c) + (b − d)i

(6 + 4i) − (3 − 2i) = 3 + 6i

4. Zero: To equal zero, a complex number must have both its real part and its imaginary part equal to zero. That is, a + bi = 0 if and only if a = 0 and b = 0.

5. Opposites: To form the opposite of a complex number, take the opposite of each part. The opposite of a + bi is −(a + bi), or −a + (−b)i. The opposite of 6 − 2i is −6 + 2i.

6. Multiplication: To form the product of two complex numbers, multiply each part of one number by each part of the other. The product of (a + bi) × (c + di) is ac + adi + bci + bdi ² . Since bdi ² = −bd, the final product is ac + adi + bci − bd. This expression can be expressed as a complex number as (ac − bd) + (ad + bc)i. Similarly, the product (5 − 2i) × (4 − 3i) is 14 − 23i.

7. Conjugates: Two numbers whose imaginary parts are opposites are called complex conjugates. The complex numbers a + bi and a − bi are complex conjugates because the terms bi have opposite signs. Pairs of complex conjugates have many applications because the product of two complex conjugates is real. For example, (6 − 12i) × (6 + 12i) = 36 − 144i ² , or 36 + 144 = 180.

8. Division: Division of complex numbers is restricted by the fact that an imaginary number cannot be divided by itself. Division can be carried out, however, if the divisor is first converted to a real number. To make this conversion, the divisor can be multiplied by its complex conjugate.

Graphical representation

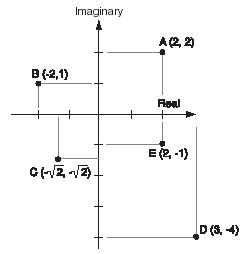
After complex numbers were discovered in the eighteenth century, mathematicians searched for ways of representing these combinations of real and imaginary numbers. One suggestion was to represent the numbers graphically, as shown in Figure 1. In graphical systems, the real part of a complex number is plotted along the horizontal axis and the imaginary part is plotted on the vertical axis. Thus, in Figure 1, point A stands for the complex number 2 + 2i and point B stands for the complex number −2 + i.

Uses of complex numbers

For all the "imaginary" component they contain, complex numbers occur frequently in scientific and engineering calculations. Whenever the solution to an equation yields the square root of a negative number (such as √−9), complex numbers are involved. One of the problems faced by a scientist or engineer, then, is to figure out what the imaginary and complex numbers represent in the real world.