Conservation laws

---

---

Photo by: Paul Fleet

Conservation laws are scientific statements that describe the amount of some quantity before and after a physical or chemical change.

Conservation of mass and energy

One of the first conservation laws to be discovered was the conservation of mass (or matter). Suppose that you combine a very accurately weighed amount of iron and sulfur with each other. The product of that reaction is a compound known as iron(II) sulfide. If you also weigh very accurately the amount of iron(II) sulfide formed in that reaction, you will discover a simple relationship: The weight of the beginning materials (iron plus sulfur) is exactly equal to the weight of the product or products of the reaction (iron(II) sulfide). This statement is one way to express the law of conservation of mass. A more formal definition of the law is that mass (or matter) cannot be created or destroyed in a chemical reaction.

A similar law exists for energy. When you turn on an electric heater, electrical energy is converted to heat energy. If you measure the amount of electricity supplied to the heater and the amount of heat produced by the heater, you will find the amounts are equal. In other words, energy is conserved in the heater. It may take various forms, such as electrical energy, heat, magnetism, or kinetic energy (the energy of an object due to its motion), but the relationship is always the same: The amount of energy used to initiate a change is the same as the amount of energy detected at the end of the change. In other words, energy cannot be created or destroyed in a physical or chemical change. This statement summarizes the law of conservation of energy.

At one time, scientists thought that the law of conservation of mass and the law of conservation of energy were two distinct laws. In the early part of the twentieth century, however, German-born American physicist Albert Einstein (1879–1955) demonstrated that matter and energy are two forms of the same thing. He showed that matter can change into energy and that energy can change into matter. Einstein's discovery required a restatement of the laws of conservation of mass and energy. In some instances, a tiny bit of matter can be created or destroyed in a change. The quantity is too small to be measured by ordinary balances, but it still amounts to something. Similarly, a small amount of energy can be created or destroyed in a change. But, the total amount of matter PLUS energy before and after a change still remains constant. This statement is now accepted as the law of conservation of mass and energy.

Examples of the law of conservation of mass and energy are common in everyday life. The manufacturer of an electric heater can tell consumers how much heat will be produced by a given model of heater. The amount of heat produced is determined by the amount of electrical current that goes into the heater. Similarly, the amount of gasoline that can be formed in the breakdown of petroleum can be calculated by the amount of petroleum used in the process. And the amount of nuclear energy produced by a nuclear power plant can be calculated by the amount of uranium-235 used in the plant.

Calculations such as these are never quite as simple as they sound. We think of an electric lightbulb, for example, as a way of changing electrical energy into light. Yet, more than 90 percent of that electricity is actually converted to heat. (Baby chicks are kept warm by the heat of lightbulbs.) Still, the conservation law holds true. The total amount of energy produced in a lightbulb (heat plus light) is equal to the total amount of energy put into the bulb in the form of electricity.

Other conservation laws

Conservation of electric charge. Most physical properties abide by conservation laws. Electric charge is another example. Electric charge is the property that makes you experience a shock or spark when you touch a metal doorknob after shuffling your feet across a rug. It is also the property that produces lightning. Electric charge comes in two varieties: positive and negative.

The law of conservation of electric charge states that the total electric charge in a system is the same before and after any kind of change. Imagine a large cloud of gas with 1,000 positive (+) charges and 950 negative (−) charges. The total electrical charge on the gas would be 1,000+ + 950−= 50+. Next, imagine that the gas is pushed together into a much smaller volume. Whatever else you may find out about this change, you can know one fact for certain: the total electric charge on the gas will continue to be 50+.

Conservation of momentum. Two of the most useful conservation laws apply to the property known as momentum. Linear momentum is defined as the product of an object's mass and its velocity. (Velocity is the rate at which the position of an object changes with time, including both the speed and the direction.) A 200-pound football player moving with a speed of 10 miles per hour has a linear momentum of 200 pounds × 10 miles per hour, or 2,000 pound-miles per hour. In comparison, a 100-pound sprinter running at a speed of 20 miles per hour has exactly the same liner momentum: 100 pounds × 20 miles per hour, or 2,000 pound-miles per hour.

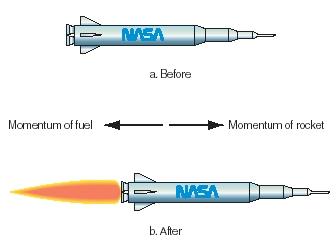
Linear momentum is consumed in any change. For example, imagine a rocket ship about to be fired into space (Figure 1a). If the rocket ship is initially at rest, its speed is 0, so its momentum must be 0. No matter what its mass is, the linear momentum of the rocket is mass × 0 miles per hour = 0. The important fact that the conservation of linear momentum tells us is that, whatever else happens to the rocket ship, its final momentum will also be 0.

What happens when the rocket is fired, then, as in Figure 1b? Hot gases escape from the rear of the rocket ship. The momentum of those gases is equal to their total mass (call that m _g ) times their velocity (v _g ), or m _g v _g . We'll give this number a negative sign (−m _g v _g ) to indicate that the gases are escaping backward, or to the left.

The law of conservation of linear momentum says, then, that the rocket has to move in the opposite direction, to the right or the + direction, with a momentum of m _g v _g . That must be true because then −m _g v _g (from the gases) plus +m _g v _g (from the rocket) = 0. If you know the mass of the rocket, you can find the speed with which it will travel to the right.

Figure 1. The rocket moves in the opposite direction of the escaping gases. (Reproduced by permission of

The Gale Group

.)

A second kind of momentum is angular momentum. The most familiar example of angular momentum is probably a figure skater spinning on the ice. The skater's angular momentum depends on three properties: her mass (or weight), the speed with which she is spinning, and the radius of her body.

At the beginning of a spin, the skater's arms may be extended outward, producing a large radius (the distance from the center of her body to the outermost part of his body). As she spins, she may pull her arms inward, bringing them to her side. What happens to the skater's angular momentum during the spin?

We can neglect the skater's mass, since she won't gain or lose any weight during the spin. The only factors to consider are the speed of her spin and her body radius. The law of conservation of angular momentum says that the product of these two quantities at the beginning of the spin (v ₁ r ₁ ) must be the same as the product of the two quantities at the end of the spin (m ₂ r ₂ ). So m ₁ r ₁ = m ₂ r ₂ must be true. But if the skater makes the radius of her body smaller, this equality can be true only if her velocity increases. This fact explains what you actually see on the ice. As a spinning skater pulls her arms in (and the body radius gets smaller), her spinning speed increases (and her velocity gets larger).

Conservation of parity. Conservation laws are now widely regarded as some of the most fundamental laws in all of nature. It was a great shock, therefore, when two American physicists, Val Lodgson Fitch (1923– ) and James Watson Cronin (1931– ), discovered in the mid-1960s that certain subatomic particles known as K-mesons appear to violate a conservation law. That law is known as the conservation of parity, which defines the basic symmetry of nature: that an object and its mirror image will behave the same way. Scientists have not yet fully explained this unexpected experimental result.