Periodic function
A periodic function is an event that occurs repeatedly in a very regular manner. Suppose that you stand on the beach near a lighthouse. As you watch, the lighthouse's beam will sweep across the landscape in a very regular pattern. You might see the beam pointing directly at you every second, or every two seconds, or at some other regular interval. The
regularity of a lighthouse beam is one of the ways in which ships at sea recognize the lighthouse and know where they are.
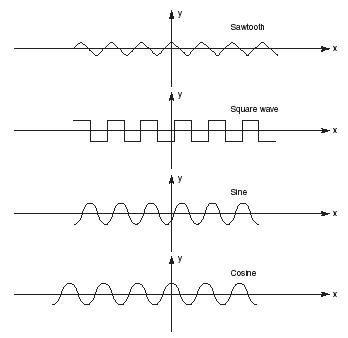
The graphical representation of a periodic function has a very characteristic shape. Figure 1 shows the most common of these shapes. In this graph, the vertical (y) axis shows the amplitude (magnitude) while the horizontal (x) axis shows time. As you go from left to right along the graph, it is as if you were moving forward in time. The origin (the point at which the two axes cross) represents zero time, and each additional second or minute or hour is represented by one unit to the right on the graph.
In the graph of the cosine, the amplitude at time zero is the highest it ever gets. If this graph represented the sweep of a lighthouse light, for example, point zero might be the time at which the light beam was pointing directly at you. As time passes (moving to the right on the x-axis), the amount of light you see (the amplitude) gradually decreases. Eventually it reaches its lowest possible point (the bottom of the curve). At that point, the light would be pointing directly away from you. Then, the light would continue its sweep until it was once more facing toward you.
One of the most important applications of periodic functions is in the study of electromagnetic radiation. Such diverse forms of energy as cosmic rays, X rays, ultraviolet light, infrared radiation, visible light, radar, radio waves, and microwaves all have one property in common: they are all periodic functions. Their properties and behavior can be studied by drawing graphical representations.