Probability theory
Probability theory is a branch of mathematics concerned with determining the likelihood that a given event will occur. This likelihood is determined by dividing the number of selected events by the number of total events possible. For example, consider a single die (one of a pair of dice) with six faces. Each face contains a different number of dots: 1, 2, 3, 4, 5, or 6. If you role the die in a completely random way, the probability of getting any one of the six faces (1, 2, 3, 4, 5, or 6) is one out of six.
Probability theory originally grew out of problems encountered by seventeenth-century gamblers. It has since developed into one of the most respected and useful branches of mathematics with applications in many different industries. Perhaps what makes probability theory most valuable is that it can be used to determine the expected outcome in any situation—from the chances that a plane will crash to the probability that a person will win the lottery.
History of probability theory
Probability theory was originally inspired by gambling problems. The earliest work on the subject was performed by Italian mathematician and physicist Girolamo Cardano (1501–1576). In his manual Liber de Ludo Aleae, Cardano discusses many of the basic concepts of probability complete with a systematic analysis of gambling problems. Unfortunately, Cardano's work had little effect on the development of probability because his manual did not appear in print until 1663—and even then received little attention.
In 1654, another gambler named Chevalier de Méré invented a system for gambling that he was convinced would make money. He decided to bet even money that he could roll at least one twelve in 24 rolls of two dice. However, when the Chevalier began losing money, he asked his mathematician friend Blaise Pascal (1623–1662) to analyze his gambling system. Pascal discovered that the Chevalier's system would lose about 51 percent of the time.
Pascal became so interested in probability that he began studying more problems in this field. He discussed them with another famous mathematician, Pierre de Fermat (1601–1665) and, together they laid the foundation of probability theory.

Methods of studying probability
Probability theory is concerned with determining the relationship between the number of times some specific given event occurs and the number of times any event occurs. For example, consider the flipping of a coin. One might ask how many times a head will appear when a coin is flipped 100 times.
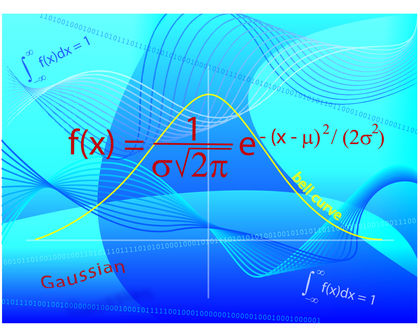
Determining probabilities can be done in two ways: theoretically and empirically. The example of a coin toss helps illustrate the difference between these two approaches. Using a theoretical approach, we reason that in every flip there are two possibilities, a head or a tail. By assuming each event is equally likely, the probability that the coin will end up heads is ½ or 0.5.
The empirical approach does not use assumptions of equal likelihood. Instead, an actual coin flipping experiment is performed, and the number of heads is counted. The probability is then equal to the number of heads actually found divided by the total number of flips.
Basic concepts
Probability is always represented as a fraction, for example, the number of times a "1 dot" turns up when a die is rolled (such as 1 out 6, or ⅙) or the number of times a head will turn up when a penny is flipped (such as 1 out of 2, or ½). Thus the probability of any event always lies somewhere between 0 and 1. In this range, a probability of 0 means that there is no likelihood at all of the given event's occurring. A probability of 1 means that the given event is certain to occur.
Probabilities may or may not be dependent on each other. For example, we might ask what is the probability of picking a red card OR a king from a deck of cards. These events are independent because even if you pick a red card, you could still pick a king.
As an example of a dependent probability (also called a conditional probability), consider an experiment in which one is allowed to pick any ball at random out of an urn that contains six red balls and six black balls. On the first try, a person would have an equal probability of picking either a red or a black ball. The number of each color is the same. But the probability of picking either color is different on the second try, since only five balls of one color remain.
Applications of probability theory
Probability theory was originally developed to help gamblers determine the best bet to make in a given situation. Many gamblers still rely on probability theory—either consciously or unconsciously—to make gambling decisions.
Probability theory today has a much broader range of applications than just in gambling, however. For example, one of the great changes that took place in physics during the 1920s was the realization that many events in nature cannot be described with perfect certainty. The best one can do is to say how likely the occurrence of a particular event might be.
When the nuclear model of the atom was first proposed, for example, scientists felt confident that electrons traveled in very specific orbits around the nucleus of the atom. Eventually they found that there was no basis for this level of certainty. Instead, the best they could do was to specify the probability that a given electron would appear in various regions of space in the atom. If you have ever seen a picture of an atom in a science or chemistry book, you know that the cloudlike appearance of the atom is a way of showing the probability that electrons occur in various parts of the atom.
finally, i found what my teacher want!
from this information, i have done my project work..thank you.
i can finally finish my research now.