Set theory

A set is a collection of things. A set can consist of real or literal numbers (such as 1, 2, 3, 4 or a, b, c, d) or of objects (such as baseballs or books). Set theory is the field of mathematics that deals with the properties of sets that are independent of the things that make up the set. For example, a mathematician might be interested in knowing about sets S and T without caring at all whether the two sets are made of baseballs, books, letters, or numbers.

The things that do to make up a set are called members or elements. In the above examples, 1, 2, 3, and 4 are members or elements of one set, and a, b, c, and d are elements of a second set.

Sets can be made of anything at all. The only characteristic they must have in common is classification together in a set. For example, the collection of all the junk at a rummage sale is a perfectly good set. These items may have little in common, except that someone has gathered them up and put them in a rummage sale. That act is enough to make the items a set.

Properties of sets

Set theory is based on a few basic definitions and fairly obvious properties of sets. The statements below summarize the most fundamental of these definitions and properties.

Definition of a set. A set is usually defined by naming it with an upper case Roman letter (such as S) followed by the elements of the set. For example, the items in a rummage sale might be indicated as S = {basketball, horseshoe, scooter, bow tie, hockey puck}, in which the braces ({}) enclose the members of the set.

Equality of sets. Two sets are said to be equal if every element in each set is also an element of the second set. In other words, two sets are equal if, and only if, they both contain the same elements.

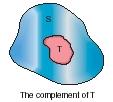
Subsets. One set (call it T) is said to be a subset of a second set (call it S) if every element in T is also contained in S AND if some elements in S are not included in T. This condition is illustrated in Figure 1. The portion of S that is not included in T is known as the complement of T. It consists of all of the elements contained in S but not contained in T. Figure 2 illustrates the idea of a complement of a set.

Union of sets. The union of two sets is defined as the collection of elements that belong to (1) either of the two sets or (2) both of the two sets. In other words, the union of the two sets corresponds to the sum of all their elements. Figure 3 shows the union of two sets, S and T.

Intersection of sets. The intersection of two sets is defined as the collection of elements that belong to both of the two sets. In Figure 4, for example, the more heavily shaded area shows the elements that are contained in both S and T. The lighter shaded areas represent elements that belong to S, but not to T, or to T, but not to S.

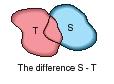
Difference of two sets. The difference between two sets is defined as the collection of elements that belong in one set but not in the other. The more darkly shaded portion of Figure 5 shows the difference S-T. Notice that it contains all of the elements of S with the exception of the small portion that also belongs to T.